Riječ fraktal skovao je Benoit Mandelbrot ‘70-ih godina, od latinskog pridjeva fractus, što znaći razlomljen, slomljen, nepovezan. Teško je dati preciznu definiciju fraktala i fraktalne geometrije. Čak je i sam Mandelbrot (kojeg bismo mogli nazvati ocem fraktalne geometrije, iako su neki takvi objekti bili poznati i puno ranije) bio neodlučan pred tim problemom, pa je za svoju definiciju fraktala, koju je bio ponudio, rekao da izuzima neke objekte koji bi se trebali zvati fraktali. Ta definicija glasila je: fraktal je skup za koji je Hausdorff-Besicović dimenzija veća od topološke dimenzije. Definicija koja bi bila nešto bolja i preciznija je ona da je fraktal objekt koji ima necjelobrojnu fraktalnu (Hausdorff-Besicović) dimenziju. Prije svega, treba naglasiti da je dimenzija jedan od onih entiteta kojima pridajemo intuitivno značenje, kao što su vrijeme, prostor, masa, itd., te je stoga nužno za preciznu definiciju fraktalnog objekta precizno definirati dimenziju.

    Topološka dimenzija je najbliža intuitivnom, prirodnom shvaćanju: točka ima topološku dimenziju 0, linija 1, ravnina 2, a prostor 3. Precizna definicija pak glasi: (Def. 4) Skup ima topološku dimenziju 0, ako svaka točka ima proizvoljno maleno susjedstvo čije granice ne sijeku skup.

Skup S ima topološku dimenziju d, ako svaka točka u S ima proizvoljno maleno susjedstvo čije granice dodiruju S u skupu s dimenzijom d-1, a d je posljednji pozitivni cijeli broj za kojeg ovo vrijedi. [8]

    Fraktalna dimenzija pak se definira na drugačiji način. Objasniti ćemo to na primjeru Cantorovog skupa (Sl. 14).

Sl. 14 - Cantorov skup, ili cesto nazivan Cantorova prašina

    Taj jednostavan fraktal izum je Georga Cantora, njemačkog matematičara, osnivača teorije skupova, koji ga je proučavao još 1872. Kako je sa slike očito, nastaje primjenom jednostavnog algoritma: uzmimo duljinu (skup točaka na duljini - recimo da je to jedinična duljina, pa je onda skup S_k=[0,1]), isjecimo središnju trećinu (tj. izbacimo točke intervala [,] iz skupa S_k), potom istu operaciju primjenimo na preostala dva odvojena dijela duljine (tj. izbacimo intervale [,] i [,]), i tako dalje. Očito je da svaka iteracija odreže skupa koji je ostao od prethodne iteracije. Duljina skupa u n-toj iteraciji tada je očito ()ⁿ, ako je početna dužina jedinična, međutim, svejedno i kada n→∞, skup ima beskonačno mnogo elemenata. Nalikuje na dužinu, ali nije dužina, smanjuje se od dužine prema točki, ali nije točka. Ono što ralikuje točku i dužinu od Cantorovog skupa jest dimenzija.

    Hausdorff-Besicovićeva definicija dimenzije glasi: (Def. 5) 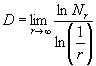. D je fraktalna dimenzija, a N_r je broj fragmenata originalnog objekta, koji su pojedinačno linearno r puta manji [3,8,9]. Za jednostavnije fraktale (kakav je Cantorov skup) limes tog razlomka jednak je samom razlomku, jer je svaka slijedeća iteracija identična prethodnoj, pa možemo pisati 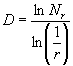. Za sam Cantorov skup fraktalna dimenzija je =0.63092975357..., manja od 1, a veća od 0. Intuitivno, to se može shvatiti da točka dimenzije 0 jako slabo ispunja prostor, slabije od Cantorovog skupa, dok linija dimenzije 1 ispunja prostor bolje od Cantorovog skupa.

    Definicija fraktalne dimenzije može se primjeniti i na “normalne” objekte. Primjerice, podjelimo li liniju na dva dijela (točno u polovištu), te desnu polovicu izbacimo iz skupa, pa ponovno svaki dio podjelimo na dva djela, izbacimo desni dio, itd., dobijamo objekt fraktalne dimenzije =0, odnosno točku. Slično se može napraviti i za liniju, ravninu i postor.

    Drugi vrlo popularni fraktal otkrila je početkom stoljeća Helge von Koch, švedska matematičarka, a nazvan je, zbog svog izgleda, Kochina pahuljica (Sl. 15).

Sl. 15 - Stvaranje Kochine pahuljice

    Čak i “od oka” se može pretpostaviti da će pahuljica imati dimenziju između jedan i dva, jer na neki način od tri linije dimenzije 1 “zalazi” u ravninu dimenzije 2, ne ispunjajući je potpuno. No, promotrimo nastanak Kochine pahuljice. Procedura je za sve tri stranice jednaka: isječemo središnju trećinu stranice (nalik na Cantorov skup), ali na prazno mjesto dodamo dvije stranice iste duljine (dakle, trećina originalne, velike stranice) pod kutem od 60^o, tako da liči na veliki, jednakostranični trokut. U slijedećoj iteraciji to učinimo sa svim novonastalim stranicama. Na Sl. 15 procedura se ponavlja pet puta. Dimenzija pahuljice je tada =1.2618595..., a duljina joj je (ako je početna stranica jedinična) nakon n iteracija 3·()ⁿ.

    Osnovna karakteristika svih fraktalnih struktura jest samosličnost, tj. sličnost oblika na svim mjerilima. Uzmimo na primjer Cantorov skup – povećamo li bilo koji njegov dio, vidjeti ćemo strukture koje potpuno sliče velikoj slici, odnosno, bilo kojoj drugoj slici u samom skupu. Kod jednostavnog fraktala kao što je Cantorov skup, ti oblici su identični, a kod složenijih fraktala obično nisu, ali ne postoji fraktal koji nije barem sličan sam sebi u manjim mjerilima. Vratimo li se bifurkacijskom dijagramu, vidjeti ćemo da je i on sam po sebi fraktal: promotrimo li podvostručenja perioda, očito je da svako slijedeće podvostručenje možemo opisati kao da nastaje iteracijom, preko Feigenbaumove konstante Δ_f, te izračunati dimenziju tih podvostručavanja, koja je između 1 i 2, dakle, fraktalna. Postoji još mnoštvo fraktalnih pojava u bifurkacijskom dijagramu, a jedna od očitih je ona prikazana na Sl. 16.

Sl. 16 - lijeva slika je u rasponu r=[2,4], x=[0,1]; desna pak u r=[3.31,3.68], x=[0.725,0.925]

    Vidimo, da su desna i lijeva slika gotovo identične, iako je lijeva slika povećani komadić desne. I lijeva slika ima svoj komadić koji je sličan cijeloj slici, i tako u beskonačnost. Kako smo već rekli da u kaotičnom režimu ima beskonačno mnogo prozora u kaosu, i da svaki od tih periodičkih atraktora u regularnim prozorima prolazi kroz bifurkacije, možemo zaključiti da u svim mogućim djelovima bifurkacijskog dijagrama postoje komadići koji su slični velikoj slici. To je jedno od osnovnih karakteristika svih fraktala.

Prethodno poglavlje          Povratak na sadržaj          Slijedeće poglavlje

Povratak na početnu stranicu          Kontakt autora